Regra de Três no Enem

Olá, pessoal! Vocês já observaram o quanto a regra de três é importante? Depois que a aprendemos na escola, podemos utilizá-la em diversas situações e até mesmo em outras disciplinas, como Química, Física e Biologia. Por essa razão, não poderíamos deixar de registrar sua importância nas provas de Matemática e suas Tecnologias do Enem. Todos os anos deparamo-nos com várias questões que podem ser resolvidas através da boa e velha Regra de Três, seja ela simples ou composta!

De modo geral, podemos afirmar que a regra de três simples é utilizada para a resolução de problemas que envolvem duas grandezas direta ou inversamente proporcionais. O nome da regra vem do fato de que relacionamos três valores conhecidos para determinar um valor procurado, que podemos chamar de quarta proporcional.

Ao resolver uma regra de três, é importante organizar os valores de acordo com o tipo da grandeza trabalhada. Vejamos um exemplo de questão sobre regra de três simples cobrada no Enem de 2012:

1º Exemplo de Questão com Regra de Três no Enem de 2012

Uma mãe recorreu à bula para verificar a dosagem de um remédio que precisava dar a seu filho. Na bula, recomendava-se a seguinte dosagem: 5 gotas para cada 2kg de massa corporal a cada 8 horas.

Se a mãe ministrou corretamente 30 gotas do remédio a seu filho a cada 8 horas, então a massa corporal dele é de:

a) 12 kg.

b) 16 kg.

c) 24 kg.

d) 36 kg.

e) 75 kg.

Resolução:

Nesse caso, temos duas grandezas importantes: as gotas e a massa da criança. Observe que o intervalo de horas de ministração do medicamento não é relevante. Vamos relacionar as grandezas em uma tabela:

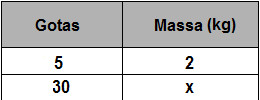
Vamos analisar: as grandezas são direta ou inversamente proporcionais? Para simplificar essa questão, colocaremos setas na tabela sempre apontando para os maiores valores. Se as setas possuírem a mesma direção, teremos grandezas diretamente proporcionais; mas se estiverem invertidas, teremos grandezas inversamente proporcionais.

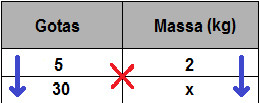
Podemos concluir que as grandezas são diretamente proporcionais, pois as duas setas têm a mesma direção. Observe o “x” em vermelho na tabela. Essa indicação nos mostra que faremos uma multiplicação cruzada.

5 = 2
30   x 

Com a multiplicação cruzada, chegamos à seguinte equação:

5 · x = 2 · 30
5 · x = 60
x = 60
      5
x = 12 kg

Portanto, a massa corporal da criança é de 12 kg, e a alternativa correta é a letra a.

Outro tipo de questão muito recorrente é o que envolve a regra de três composta. Diferentemente da simples, esta envolve três ou mais grandezas direta ou inversamente proporcionais. A resolução da regra de três composta só se difere porque, ao organizar os dados do problema em uma tabela, montamos uma equação em que um membro possui os elementos da coluna em que aparece a incógnita, e o outro membro da igualdade é o produto dos elementos da demais colunas.

Vamos agora analisar uma questão de regra de três composta cobrada na prova do Enem de 2013:

2º Exemplo de Questão com Regra de Três no Enem de 2013

Uma indústria tem um reservatório de água com capacidade para 900 m³. Quando há necessidade de limpeza do reservatório, toda a água precisa ser escoada. O escoamento da água é feito por seis ralos, e dura 6 horas quando o reservatório está cheio. Esta indústria construirá um novo reservatório, com capacidade de 500 m³, cujo escoamento da água deverá ser realizado em 4 horas, quando o reservatório estiver cheio. Os ralos utilizados no novo reservatório deverão ser idênticos aos do já existente.

A quantidade de ralos do novo reservatório deverá ser igual a

a) 2.

b) 4.

c) 5.

d) 8.

e) 9.

Resolução:

Temos aqui três grandezas: a capacidade do reservatório, a quantidade de ralos e o tempo em horas. Vamos relacionar essas grandezas em uma tabela:

Agora verificaremos se as grandezas são direta ou inversamente proporcionais. Novamente colocaremos setas na tabela, sempre apontando para os maiores valores.

Temos duas grandezas diretamente proporcionais (capacidade e ralos) e uma inversamente proporcional (tempo). Sempre que houver valores inversamente proporcionais, eles deverão ser “invertidos”. Para montar a equação, colocaremos os valores da coluna “ralos” iguais ao produto da coluna “capacidade” pelo inverso da coluna “tempo”, isto é:

ralos = capacidade · “inverso de tempo”

6 = 900 . 4
x    500   6

Simplificando a fração ⁹⁰⁰/₅₀₀ por 100, e a fração ⁴/₆ por 2, teremos:

6 = 9 . 2
x    5   3

6 = 18
x    15

Faremos agora a multiplicação cruzada:

18 · x = 6 · 15
18 · x = 90
x = 90
     18
​x = 5 ralos

Portanto, o novo reservatório deverá ter cinco ralos, e a alternativa correta é a letra c.