Olá, galera! Já perceberam que nas provas anteriores do Enem sempre aparecem algumas questões que envolvem o cálculo de média aritmética? A nossa dica do dia é para garantir que você não erre na resolução dessas questões! Para isso, vamos relembrar como é que se calcula essa importante medida de tendência central.
A média aritmética (MA) é calculada a partir da soma de alguns valores dividida pela quantidade de termos somados. Por exemplo, um professor pretende calcular a nota média obtida por seus alunos no 1° bimestre. Suponha que a turma possua n alunos, a média aritmética é dada pela soma de todas as notas dividida pela quantidade de alunos:
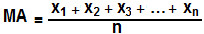
Em Estatística, uma variação muito comum da média é a média aritmética ponderada (MP). Esta apresenta um fator de ponderação, também chamado de peso. Vejamos um exemplo: Na escola de João, o professor de Matemática utiliza pesos para calcular a média dos alunos. Suponha que o professor utilize peso 2 na prova 1 (p1), peso 3 no trabalho (t), peso 3 nas atividades (a) e peso 4 na prova 2 (p2), qual seria a fórmula para calcular a média? Utilizando a fórmula para o cálculo da média aritmética ponderada, temos:
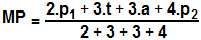
Considere p como os pesos e x como os valores de uma variável. De forma geral, podemos caracterizar o cálculo da média ponderada como:
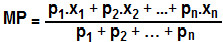
Vejamos agora alguns exemplos de como aparecem as questões de média aritmética no Enem:
1ª Questão com média aritmética no Enem de 2013
As notas de um professor que participou de um processo seletivo, em que a banca avaliadora era composta por cinco membros, são apresentadas no gráfico. Sabe-se que cada membro da banca atribuiu duas notas ao professor, uma relativa aos conhecimentos específicos da área de atuação e outra, aos conhecimentos pedagógicos, e que a média final do professor foi dada pela média aritmética de todas as notas atribuídas pela banca avaliadora.
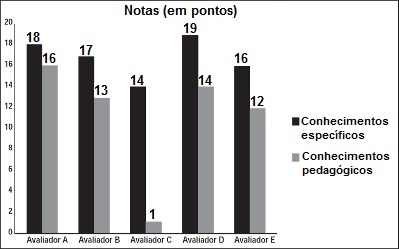
1ª questão com média aritmética – Enem 2013
Utilizando um novo critério, essa banca avaliadora resolveu descartar a maior e a menor notas atribuídas ao professor.
A nova média, em relação à média anterior, é:
a) 0,25 ponto maior.
b) 1,00 ponto maior.
c) 1,00 ponto menor.
d) 1,25 ponto maior.
e) 2,00 pontos menor.
Resolução:
Primeiramente vamos realizar o cálculo da média aritmética de todas as 10 notas recebidas pelo professor:
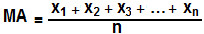
MA = 18 + 16 + 17 + 13 + 14 + 1 + 19 + 14 + 16 + 12
10
MA = 140
10
MA = 14
Se descartarmos a maior e a menor nota, retiraremos as notas de valor 19 e 1. Portanto, o cálculo da média aritmética agora será dado por 8 notas:
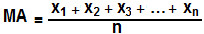
MA = 18 + 16 + 17 + 13 + 14 + 14 + 16 + 12
8
MA = 120
8
MA = 15
Podemos então concluir que, retirando as notas mais extremas, a média passou de 14 para 15 pontos, ficando 1,00 ponto maior. Logo, a alternativa correta é a letra b.
2ª Questão com média aritmética no Enem de 2012
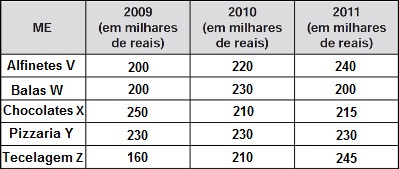
A tabela a seguir mostra a evolução da receita bruta anual nos três últimos anos de cinco microempresas (ME) que se encontram à venda.
2ª questão com média aritmética – Enem 2012
Um investidor deseja comprar duas das empresas listadas na tabela. Para tal, ele calcula a média da receita bruta anual dos últimos três anos (de 2009 até 2011) e escolhe as duas empresas de maior média anual.
As empresas que este investidor escolhe comprar são
a) Balas W e Pizzaria Y.
b) Chocolates X e Tecelagem Z.
c) Pizzaria Y e Alfinetes V.
d) Pizzaria Y e Chocolates X.
e) Tecelagem Z e Alfinetes V.
Resolução:
Para descobrir quais são as microempresas com maior média anual, vamos analisar as médias de cada empresa:
Alfinetes V:
MaV = 200 + 220 + 240
3
MaV = 220
Balas W:
MaW = 200 + 230 + 200
3
MaW = 210
Chocolates X:
MaX = 250 + 210 + 215
3
MaX = 225
Pizzaria Y:
MaY = 230 + 230 + 230
3
MaY = 230
Tecelagem Z:
MaZ = 160 + 210 + 245
3
MaZ = 205
Através dos cálculos das médias, podemos constatar que as microempresas que apresentam as maiores médias anuais são a Chocolates X e Pizzaria Y, portanto, a alternativa que apresenta a porcentagem correta é a letra d.
Bons estudos!







