Olá, pessoal! Nas últimas avaliações do Exame Nacional do Ensino Médio (Enem), as provas de “Matemática e suas Tecnologias” estão cobrando com frequência questões que envolvem o conhecimento em probabilidade. Em geral, as questões de probabilidade no Enem baseiam-se em ideias simples que não exigem um grande conhecimento de fórmulas matemáticas. Normalmente as situações propostas tratam de experimentos aleatórios e também de casos equiprováveis, isto é, os eventos possuem probabilidades iguais de ocorrência.
As questões de probabilidade no Enem baseiam-se na interpretação das ideias apresentadas e no uso do cálculo das chances de um evento acontecer, o qual é representado pela fórmula:
p(E) = n(E) = número de casos favoráveis
n(Ω) número de casos possíveis
O número de casos favoráveis é justamente o que “estou procurando”, e o número de casos possíveis é também conhecido como o espaço amostral, sendo representado pela letra grega ômega (Ω). Vejamos dois exemplos de questões com probabilidade no Enem de provas anteriores.
1ª Questão com probabilidade no Enem de 2011
Todo o país passa pela primeira fase de campanha de vacinação contra a gripe suína (H1N1). Segundo um médico infectologista do Instituto Emílio Ribas, de São Paulo, a imunização “deve mudar”, no país, a história da epidemia. Com a vacina, de acordo com ele, o Brasil tem a chance de barrar uma tendência do crescimento da doença, que já matou 17 mil no mundo. A tabela apresenta dados específicos de um único posto de vacinação.
.jpg)
Questão sobre Probabilidade no Enem de 2011
Escolhendo-se aleatoriamente uma pessoa atendida nesse posto de vacinação, a probabilidade de ela ser portadora de doença crônica é
a) 8%.
b) 9%.
c) 11%.
d) 12%.
e) 22%.
De acordo com a tabela apresentada no exercício, temos informações a respeito de cinco tipos de público-alvo. O total formado por esses cinco grupos compõe o nosso espaço amostral. Vamos então somar e encontrar o total de pessoas vacinadas:
n(Ω) = 42 + 22 + 56 + 30 + 50
n(Ω) = 200
Então o grupo total de vacinados são 200 pessoas. Precisamos agora do número de casos favoráveis. Essa informação é a que mais nos interessa, a quantidade de pessoas portadoras de doenças crônicas que foram vacinadas. De acordo com a tabela, esse valor é de 22 pessoas. Vamos então utilizar a fórmula para o cálculo da probabilidade:
p(E) = n(E)
n(Ω)
p(E) = 22
200
p(E) = 11
100
Fazendo a divisão de 11 por 100, encontramos o valor de 0,11. Multiplicando esse valor por 100, encontramos a porcentagem que procurávamos, 11%. Portanto, a alternativa correta é a letra c.
2ª Questão com probabilidade no Enem de 2013
Numa escola com 1 200 alunos foi realizada uma pesquisa sobre o conhecimento desses em duas línguas estrangeiras, inglês e espanhol. Nessa pesquisa constatou-se que 600 alunos falam inglês, 500 falam espanhol e 300 não falam qualquer um desses idiomas. Escolhendo-se um aluno dessa escola ao acaso e sabendo-se que ele não fala inglês, qual a probabilidade de que esse aluno fale espanhol?
a) 1
2
b) 5
8
c) 1
4
d) 5
6
e) 5
14
Assim como havíamos comentado no início, esse é o tipo de questão em que o raciocínio e a interpretação são fundamentais. Se somarmos o número de alunos que falam inglês, os que falam espanhol e os que não falam nenhuma dessas línguas, teremos um total de 1400, o que supera a quantidade de alunos da escola! Isso nos garante então que há alunos que falam inglês e espanhol simultaneamente. Vamos então determinar essas quantidades com exatidão.
Se temos 1200 alunos na escola e 300 deles não falam línguas estrangeiras, restam apenas 900 alunos que falam essas línguas. Se somarmos a quantidade de alunos que falam inglês (600) com os que falam espanhol (500), obteremos um total de 1.100. Então, ao fazermos a diferença desse total com a quantidade que fala língua estrangeira, isto é, 1.100 – 900, obteremos 200. Essa é a quantidade de alunos que falam as duas línguas. Portanto, de 600 alunos, apenas 400 falam somente inglês, e de 500 alunos, apenas 300 falam apenas espanhol. Para facilitar o entendimento, podemos organizar essas informações em um diagrama de Venn:
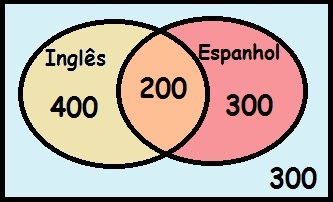
Através do Diagrama de Venn, podemos ver a distribuição dos alunos em relação à língua estrangeira falada
Através do diagrama de Venn, fica evidente que 400 alunos falam apenas inglês, 300 alunos falam apenas espanhol, 200 alunos falam as duas línguas e 300 alunos não falam nenhuma língua estrangeira.
Se vamos escolher um aluno que não fala inglês, nosso espaço amostral será composto por aqueles que falam apenas espanhol ou que não falam nenhuma língua, logo, n(Ω) = 600. O número de casos favoráveis é a quantidade de alunos que falam apenas espanhol, então n(E) = 300. Vamos então calcular a probabilidade:
p(E) = n(E)
n(Ω)
p(E) = 300
600
p(E) = 3
6
p(E) = 1
2
Portanto, a alternativa correta é a letra a.
Bons estudos!







