Olá, pessoal! As últimas provas de “Matemática e suas Tecnologias” do Exame Nacional do Ensino Médio (Enem) têm cobrado, com frequência, o conhecimento sobre Progressões Aritméticas (PA). Vamos relembrar alguns conceitos importantes para que não restem dúvidas na resolução de questões que envolvam progressão aritmética no Enem.
Primeiramente, podemos classificar uma progressão aritmética em crescente, decrescente ou constante. Uma PA é dita crescente se a sua razão é positiva, decrescente, se a sua razão é negativa; e constante, se a razão é igual a zero.
Mas como identificar a razão de uma PA? Ela pode ser obtida pela diferença entre qualquer termo da progressão e seu antecessor. Normalmente, a razão é chamada de r. Seja a seguinte progressão aritmética: A = (a1, a2, a3, …, an-1, an), representamos a razão como r = an – an-1.
Em geral, para resolver questões sobre PA no Enem, não podemos esquecer duas fórmulas muito importantes:
-
Termo geral da PA
an = a1 + (n – 1).r
-
Soma dos termos de uma PA finita
Sn = (a1 + an).n
2
Nessas fórmulas, an é o n-ésimo termo da PA, a1 é o primeiro termo, r é a razão e Sn é o valor da soma de todos os termos da progressão.
Agora que já nos recordamos de todos os pontos importantes no estudo de progressões aritméticas, vamos praticar as progressões, vendo como apareceram questões sobre PA no Enem nas provas anteriores.
Questão com progressão aritmética no Enem de 2010
Uma professora realizou uma atividade com seus alunos utilizando canudos de refrigerante para montar figuras, onde cada lado foi representado por um canudo. A quantidade de canudos (C) de cada figura depende da quantidade de quadrados (Q) que formam cada figura. A estrutura de formação das figuras está representada a seguir:
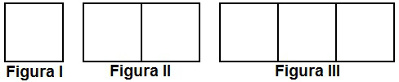
1ª questão com progressão aritmética – Enem 2010
Que expressão fornece a quantidade de canudos em função da quantidade de quadrados de cada figura?
a) C = 4Q.
b) C = 3Q + 1.
c) C = 4Q – 1
d) C = Q + 3.
e) C = 4Q – 2.
Resolução:
Para formar um quadrado, é necessário utilizar quatro canudos. Para formar dois quadrados, sete canudos e, para formar três quadrados, 10 canudos. Vejamos na tabela a seguir a distribuição dos canudos em relação à quantidade de quadrados:
|
N° de quadrados (Q) |
Quantidade de Canudos (C) Não pare agora... Tem mais depois da publicidade ;) |
|
1 |
4 |
|
2 |
7 |
|
3 |
10 |
Os números que identificam a quantidade de canudos descrevem uma progressão aritmética de razão 3. Utilizaremos aqui a fórmula do termo geral, que nos ajudará a caminhar para a solução. Vamos identificar o n-ésimo termo da PA (4, 7, 10):
an = a1 + (n – 1).r
an = 4 + (n – 1).3
Mas de acordo com o problema, podemos reescrever essa fórmula. Considerando que Q representa as posições n da progressão e C representa cada termo an da PA, temos:
C = 4 + (Q – 1).3
C = 4 + 3Q – 3
C = 3Q + 1
A alternativa correta é a letra b.
Questão com progressão aritmética no Enem de 2013
As projeções para a produção de arroz no período de 2012-2021, em uma determinada região produtora, apontam para uma perspectiva de crescimento constante da produção anual. O quadro apresenta a quantidade de arroz, em toneladas, que será produzida nos primeiros anos desse período, de acordo com essa projeção.
|
Ano |
Projeto da Produção (t) |
|
2012 |
50,25 |
|
2013 |
51,50 |
|
2014 |
52,75 |
|
2015 |
54,00 |
A quantidade total de arroz, em toneladas, que deverá ser produzida no período de 2012 a 2021 será de
a) 497,25.
b) 500,85.
c) 502,87.
d) 558,75.
e) 563,25.
Resolução:
Através do quadro, podemos identificar uma progressão aritmética formada pelos números que compõem a coluna “Projeto da Produção (t)”. O a1 = 50,25 e o a2 = 51,50, sendo que o a1 refere-se ao ano de 2012, o a2, ao ano de 2013 e assim por diante. Precisamos identificar o 10° termo, aquele que se refere ao ano de 2021. Vamos procurar a razão (r) dessa PA:
r = a2 – a1
r = 51,50 – 50,25
r = 1,25
Agora que conhecemos a razão, vamos identificar o termo a10 através da fórmula do termo geral:
an = a1 + (n – 1).r
a10 = 50,25 + (10 – 1).1,25
a10 = 50,25 + 9.1,25
a10 = 50,25 + 11,25
a10 = 61,50
Identificado que o a10 é 61,50, podemos utilizar a fórmula da soma dos termos de uma PA finita para saber a produção total do período 2012 – 2021:
Sn = (a1 + an).n
2
S10 = (50,25 + 61,50).10
2
S10 = 111,75.10
2
S10 = 1117,5
2
S10 = 558,75
Portanto, a alternativa correta é a letra d.
Bons estudos!







