Olá, pessoal! Todos aqueles que estão estudando para a prova de Matemática e suas Tecnologias devem ter observado que são vários os tópicos relacionados com a trigonometria. Hoje vamos voltar nossa atenção para um desses tópicos: as relações de seno, cosseno e tangente.
Essas razões trigonométricas encontradas no triângulo retângulo têm sido bastante recorrentes nas questões do Enem, sendo que ora o triângulo aparece bem caracterizado, ora temos que identificá-lo para aplicar as razões trigonométricas.
Você deve lembrar que um triângulo retângulo é formado por dois catetos e uma hipotenusa, além de um ângulo reto e dois ângulos agudos. Na figura a seguir temos alguns exemplos de triângulos retângulos, nos quais as hipotenusas estão destacadas de vermelho, e os catetos, de preto.
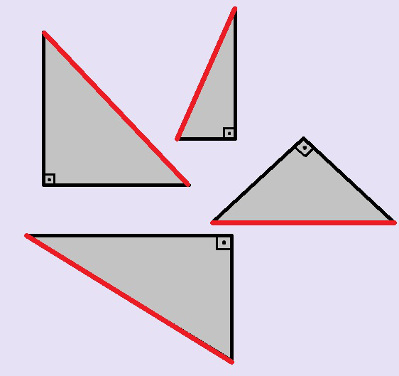
Exemplos de triângulos retângulos. Os lados vermelhos correspondem à hipotenusa, e os lados pretos, aos catetos
Para aplicar as razões métricas, é necessário saber identificar quais são os catetos referentes a cada ângulo agudo. Podemos utilizar como regra que o ângulo que estamos analisando sempre é formado pelo encontro da hipotenusa com seu cateto adjacente e que o lado do triângulo que não está formando o ângulo estudado é o cateto oposto. A hipotenusa, é claro, é o lado oposto ao ângulo reto. Observe essa análise aplicada nos triângulos a seguir:
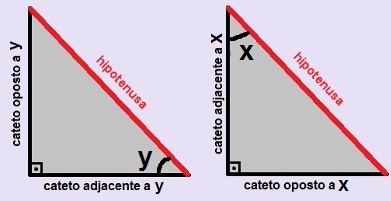
Análise dos lados do triângulo retângulo em relação aos ângulos
Vejamos agora as razões trigonométricas para o triângulo retângulo:
Seno: sen x = cateto oposto a x
hipotenusa
Cosseno: cos x = cateto adjacente a x
hipotenusa
Tangente: tg x = cateto oposto a x
cateto adjacente a x
Que tal conferir como aparecem as questões sobre seno, cosseno e tangente no Enem? Através da resolução de duas questões de edições anteriores, você poderá tirar suas dúvidas!
1ª Questão com seno, cosseno e tangente no Enem de 2013
As torres Puerta de Europa são duas torres inclinadas uma contra a outra, construídas numa avenida de Madri, na Espanha. A inclinação das torres é de 15° com a vertical e elas têm, cada uma, uma altura de 114 m (a altura é indicada na figura como o segmento AB). Estas torres são um bom exemplo de um prisma oblíquo de base quadrada e uma delas pode ser observada na imagem.
.jpg)
1ª questão com seno, cosseno e tangente – Enem 2013
Disponível em: www.flickr.com. Acesso em: 27 mar. 2012.
Utilizando 0,26 como valor aproximado para a tangente de 15° e duas casas decimais nas operações, descobre-se que a área da base desse prédio ocupa na avenida um espaço:
a) menor que 100m².
b) entre 100 m² e 300 m².
c) entre 300 m² e 500 m².
d) entre 500 m² e 700 m².
e) maior que 700 m².
Resolução:
Vamos analisar o triângulo formado pela inclinação desse prédio:
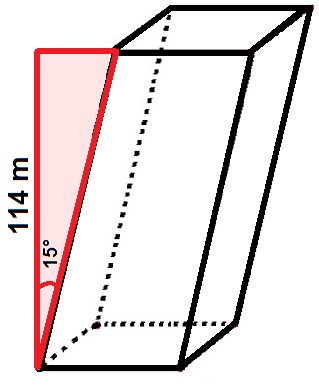
Triângulo vermelho formado pela inclinação da torre
Podemos considerar que a altura do prédio corresponde ao cateto oposto ao ângulo de 15°, já a base corresponde ao cateto adjacente. Sendo assim, podemos utilizar a fórmula da tangente para determinar essa base:
tg 15° = cateto oposto
cateto adjacente
tg 15° = x
114
Considerando que tg 15° = 0,26, como propõe o enunciado, temos:
0,26 = x
114
x = 114 . 0,26
x = 29,64 m
Como a base do prédio é quadrada, basta multiplicar o valor do lado encontrado por ele mesmo para encontrar a área da base:
A = 29,64 . 29,64
A = 878,53 m²
A alternativa correta é a letra e.
2ª Questão com seno, cosseno e tangente no Enem de 2009
Ao morrer, o pai de João, Pedro e José deixou como herança um terreno retangular de 3 km x 2 km que contém uma área de extração de ouro delimitada por um quarto de círculo de raio 1 km a partir do canto inferior esquerdo da propriedade. Dado o maior valor da área de extração de ouro, os irmãos acordaram em repartir a propriedade de modo que cada um ficasse com a terça parte da área de extração, conforme mostra a figura.
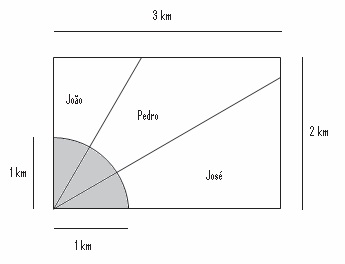
2ª questão com seno, cosseno e tangente – Enem 2013
Em relação à partilha proposta, constata-se que a porcentagem da área do terreno que coube a João corresponde, aproximadamente, a
(Considere 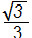 = 0,58)
= 0,58)
a) 50%
b) 43%
c) 37%
d) 33%
e) 19%
Resolução:
A área total de extração do terreno corresponde a um quarto de círculo de raio de 1 km, cujo ângulo central é de 90°. Se os irmãos pretendem dividir a área de extração de forma igualitária, então o ângulo central do terreno de cada herdeiro deverá ser de 30°, uma vez que 90 dividido por três 3 é igual a 30. Vamos então analisar a figura que representa o terreno de João:
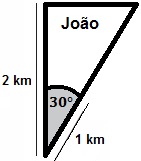
Terreno de João
Nós conhecemos apenas um dos lados do terreno de João, o cateto adjacente ao ângulo de 30°. Para que possamos calcular a área desse triângulo, é importante encontrar a medida do cateto oposto ao ângulo de 30°. Para tanto, vamos utilizar a fórmula para o cálculo da tangente:
tg 30° = cateto oposto
cateto adjacente
tg 30° = x
2
√3 = x
3 2
Utilizando a informação cedida pelo exercício, substituiremos 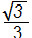 por 0,58:
por 0,58:
0,58 = x
2
x = 0,58 . 2
x = 1,16 km
Agora podemos calcular a área do terreno de João. Para isso, considere 2 km como a altura do triângulo e 1,16 km como sua base:
A = base . altura
2
A = 2 . 1,16
2
A = 1,16 km²
Para encontrar a área total do terreno deixado de herança pelo pai, basta multiplicar a base pela altura do retângulo da primeira imagem, isto é, 3 . 2 = 6 km². Para calcular a porcentagem correspondente a João, devemos encontrar o quociente entre as áreas do terreno dele e do terreno total, isto é:
P = 1,16 = 0,19333... = 19,3%
6
Portanto, a alternativa que apresenta a porcentagem correta é a letra e.
Bons estudos!







