Olá, galera! Quem aqui já está craque em resolver equações do 2° grau? Vocês sabiam que é grande a chance de cair questões sobre esse assunto na prova de Matemática e suas Tecnologias do Enem? Vamos então relembrar um pouquinho desse tema para que você não tenha nenhuma dúvida na hora de resolver a prova!
Toda equação em que o maior expoente da variável é dois é chamada de equação do 2° grau. Mas, para simplificar, dizemos que uma equação do 2° grau é do tipo ax² + bx + c = 0. Nessa equação, x é a variável, e a, b e c são coeficientes reais da equação, com a ≠ 0. A forma padrão de resolver qualquer equação do 2° grau é através da Fórmula de Bhaskara. Para tanto, devemos substituir os coeficientes da equação na fórmula a seguir:
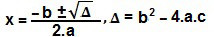
Em sua prova do Enem, podem cair também equações do 2° grau incompletas, que ocorrem quando os coeficientes b ou c são nulos. Nesse caso, além da fórmula de Bhaskara, podemos resolver a equação de outra forma.
Se b = 0:
ax² + c = 0
ax² = – c
x² = – c
a
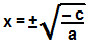
Se c = 0:
ax² + bx = 0
x · (ax + b) = 0
x' = 0
x'' = – b
a
E se, por acaso, b = c = 0, o resultado é sempre x = 0, como podemos ver a seguir:
ax² = 0
x² = 0
a
x = 0
Agora que já recordamos como se resolvem os diferentes tipos de equações do 2° grau, vejamos alguns exemplos resolvidos de questões de exames anteriores do Enem:
1ª Questão com equação do 2° grau no Enem de 2009
Um fazendeiro doa, como incentivo, uma área retangular de sua fazenda para seu filho, que está indicada na figura como 100% cultivada. De acordo com as leis, deve-se ter uma reserva legal de 20% de sua área total. Assim, o pai resolve doar mais uma parte para compor a reserva para o filho, conforme a figura.
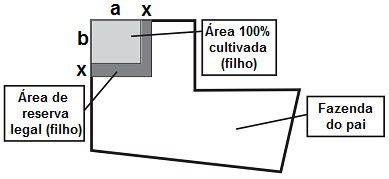
Figura de questão do Enem 2009
De acordo com a figura acima, o novo terreno do filho cumpre a lei, após acrescentar uma faixa de largura x metros contornando o terreno cultivado, que se destinará à reserva legal (filho). O dobro da largura x da faixa é
a) 10% (a + b)²
b) 10% (a · b)²
c)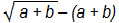
d)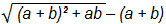
e)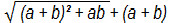
Resolução:
O terreno total do filho tem dimensões de a + x e b + x. Para calcular essa área (A), basta multiplicar essas medidas dos lados:
A = (a + x) · (b + x)
A = ab + ax + bx + x²
A = x² + x · (a + b) + ab
Se 20% da área total é de reserva legal, então 80% da área total é cultivada. Vamos então aplicar esses 80% na equação da área:
80% A = 0,8 · [x² + x · (a + b) + ab]
Mas observe que a área cultivada é representada na imagem como o quadrado de dimensões a e b. Facilmente podemos afirmar que a área desse espaço é de a · b. Vamos substituir essa multiplicação na equação anterior, em que temos 80% A (área cultivada):
a · b = 0,8 · [x² + x · (a + b) + ab]
ab = 0,8x² + 0,8x · (a + b) + 0,8ab
0,8x² + 0,8x · (a + b) + 0,8ab – ab = 0
0,8x² + 0,8x · (a + b) – 0,2ab = 0
O resultado deu origem a uma equação do 2° grau. Para facilitar nossos cálculos, vamos multiplicar toda a equação por 5:
4x² + 4(a + b) · x – ab = 0
Resolveremos essa equação através da fórmula de Bhaskara. Para evitar confusão entre os coeficientes da equação e as letras dessas fórmulas, eles serão colocados em letra maiúscula. Os coeficientes são A = 4, B = 4(a + b) e C = – ab. Substituindo-os na fórmula, teremos:
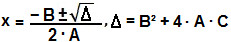
∆ = B² – 4.A.C
∆ = [4(a + b)]² – 4.4.(– ab)
∆ = 16(a + b)² + 16ab
∆ = 16 [(a + b)² + ab]
x = – B ± √∆
2.A
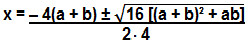
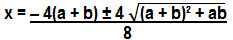
Dividindo o numerador e o denominador por 4:
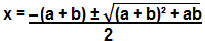
Essa equação só pode ser simplificada até aqui. A questão pede “o dobro da da largura x”, por isso multiplicaremos x por 2:
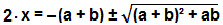
Que equivale a:
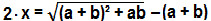
O que nos garante que a alternativa correta é a letra d.
2ª Questão com equação do 2° grau no Enem de 2013
A temperatura T de um forno (em graus centígrados) é reduzida por um sistema a partir do instante de seu desligamento (t = 0) e varia de acordo com a expressão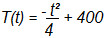 
com t em minutos. Por motivos de segurança, a trava do forno só é liberada para abertura quando o forno atinge a temperatura de 39 ºC. Qual o tempo mínimo de espera, em minutos, após se desligar o forno, para que a porta possa ser aberta?
a) 19,0.
b) 19,8.
c) 20,0.
d) 38,0.
e) 39,0.
Resolução:
De acordo com o enunciado, temos a equação 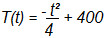e a informação de que o forno só pode ser aberto quando T = 39. Vamos igualar a equação a esse valor:
– t² + 400 = 39
4
Novamente, para facilitar os cálculos, multiplicaremos toda a equação por 4:
– t² + 1600 = 156
– t² = – 1444
Multiplicando toda a equação por (– 1), teremos a seguinte equação do 2° grau incompleta:
t² = 1444
t = √1444
t = ± 38
Como estamos procurando um valor para o “tempo”, podemos desconsiderar a resposta negativa. Portanto, t = 38, e a resposta correta é a alternativa d.
Confira mais alguns exercícios sobre equações do 2° grau! Bons estudos!
